Le Bayes-O-Matic : les réseaux bayésiens pour tous

Dans cet article, je voudrais faire un retour sur les probabilités Bayésiennes et leur interprétation épistémologique, ainsi que présenter un petit projet d'été lié à tout ça. Un outil facilitant l'utilisation de Réseaux Bayésiens dans ce contexte : le Bayes-O-Matic.

Probabilités Bayésiennes et épistémologie

Comme je l'avais vaguement suggéré dans mon précédent article sur les probabilités, dans un contexte Bayésien les probabilités prennent une interprétation assez différente du sens habituellement enseigné, pour n'avoir plus qu'un très faible lien avec le hasard.

En effet, ici, sachant une proposition $A$, $p(A)$ représente alors notre degré de croyance dans le fait que $A$ est vrai. $p(A) = 1$ impliquerait une certitude absolue dans le fait que $A$ est vraie, alors que $p(A) = 0$ une certitude absolue dans sa fausseté. Similairement, $p(A) = 0.5$ signifie que l'on a aucun indice pour juger de si $A$ est vraie ou fausse.

Dans ce contexte, le théorème de Bayes prend un rôle central : il devient la formule permettant de mettre à jour ses croyances au vu de nouveaux indices, ou de nouvelles observations. Si je veux tester une hypothèse $H$, pour laquelle j'ai a piori une croyance $p(H)$, je vais faire une expérience qui va me fournir une observation $O$, et il me faut donc ensuite mettre à jour ma croyance en $H$ au vu de cette observation, et déterminer $p(H | O)$. Pour se faire je peux utiliser le théorème de Bayes :

$$p(H|O) = \frac{p(O|H)}{p(O)}p(H) \tag{1.1}$$

Ici les trois termes de droite ont chacun un sens particulier :

• $p(H)$ est ma croyance en $H$ a priori, avant de faire l'expérience.
• $p(O|H)$ est un terme mesurant à quel point je me serais attendu à observer $O$ si je savais que $H$ était vrai. Ce terme s'évalue typiquement avec une expérience de pensée.
• $p(O)$ mesure à quel point je m'attendais à observer $O$ indépendamment de savoir si $H$ est vraie ou non, on peut également le reformuler ainsi : $p(O) = p(O|H)p(H) + p(O|\neg H)p(\neg H)$

Cet article se focalise sur l'utilisation en pratique du théorème de Bayes et sur des méthodes pour se faciliter la tâche en l'utilisant, plutôt que sur sa justification profonde, à laquelle je m'attaquerai plus tard.

Si vous voulez en savoir plus sur le Bayésianisme en général, je peux vous recommander les références suivantes :

• Les vidéos Youtube d'Hygiène Mentale sur la question : La Pensée Bayésienne, Le Sophisme du Procureur (et quelques autres leçons Bayésiennes)
• Les vidéos Youtube de Monsieur Phi sur le théorème de Bayes: La loi de Bayes (1/2), La loi de Bayes (2/2)
• La série de Lê sur Youtube : Le bayésianisme : une philosophie universelle du savoir ainsi que son livre La formule du savoir.

Cotes pour faciliter la manipulation

Ce terme $p(O)$ est souvent complexe à évaluer, et on va généralement chercher à l'éviter. Ce qui peut typiquement être fait en regardant plutôt la cote de $H$ : $\frac{p(H)}{p(\neg H)}$. Elle représente à quel point on a plus confiance dans la véracité de $H$ que dans sa fausseté. Ce ratio a également le mérite d'être plus parlant que les probabilités brutes, pour lesquelles on a du mal à interpréter les valeurs très proches de 0 ou 1.

Le théorème de Bayes exprimé en cotes est également plus facile à interpréter :

$$\frac{p(H|O)}{p(\neg H|O)} = \frac{p(O|H)}{p(O|\neg H)} \frac{p(H)}{p(\neg H)} \tag{1.2}$$

La mise à jour de notre croyance en $H$ est simplement faite en multipliant sa cote par $\frac{p(O|H)}{p(O|\neg H)}$, terme que l'on nomme le facteur de Bayes associé à l'observation $O$.

Si il était beaucoup moins surprenant d'observer $O$ si $H$ était vraie plutôt que fausse, alors $p(O|H)$ sera significativement plus grand que $p(O|\neg H)$, et le facteur de Bayes sera donc plus grand que 1. La cote de $H$ augmente, et on devient plus confiant dans sa véracité. À l'inverse, si la fausseté de $H$ prédisait $O$ avec une plus grande confiance que sa véracité, alors le facteur de Bayes serait plus petit que 1 et la cote de $H$ diminuerait.

On peut noter que c'est ici la différence fondamentale entre la méthode scientifique fréquentiste et la la méthode Bayésienne : là où la méthode fréquentiste se focalise sur la prédiction de l'hypothèse nulle $p(O|H_0)$, la méthode Bayésienne accorde autant de poids aux prédictions des différentes hypothèses, mais en les pondérant par nos croyances a priori dans chacune d'elles.

Dans un contexte où on voudrait comparer plusieurs hypothèses $H_1$, $H_2$, $H_3$, … Il peut être très accomodant de travailler avec les cotes relatives des hypothèses les unes par rapport aux autres : $\frac{p(H_i)}{p(H_j)}$, permettant au théorème de Bayes de garder une forme simple :

$$\frac{p(H_i|O)}{p(H_j|O)} = \frac{p(O|H_i)}{p(O|H_j)} \frac{p(H_i)}{p(H_j)} \tag{1.3}$$

Dans cette représentation il est possible de prendre des libertés avec le formalisme des probabilités : par exemple si je multiplie tous les termes en $p(H_i | O)$ par une même constante, l'égalité reste vraie. Lorsque l'on manipule des cotes, la normalization des probabilités n'est plus nécessaire, car seul leurs ratios a de l'importance.

On peut donc encore simplifier notre manipulation en travaillant hypothèse par hypothèse. Ici je vais noter $\mathcal{P}$ des probabilités qui ne sont pas normalisées. On ne peut qu'interpréter leurs ratios et non leurs valeurs directement. La mise à jour d'une probabilité non normalisée se fait simplement en la multipliant par son terme d'expérience de pensée (qui n'a lui non plus pas besoin d'être normalisé, tant que les ratios restent corrects) :

$$\forall i : \mathcal{P}(H_i | O) = \mathcal{P}(O | H_i) \mathcal{P}(H_i) \tag{1.4}$$

De ces probabilités non normalisées, on peut simplement récupérer les cotes et probabilités qui nous intéressent à la fin du calcul :

$$ p(H_i | O) = \frac{\mathcal{P}(H_i | O)}{\sum_j \mathcal{P}(H_j | O)} \quad ; \quad \frac{p(H_i | O)}{p(H_j | O)} = \frac{\mathcal{P}(H_i | O)}{\mathcal{P}(H_j | O)} \quad ; \quad \frac{p(H_i | O)}{p(\neg H_i | O)} = \frac{\mathcal{P}(H_i | O)}{\sum_{j \neq i} \mathcal{P}(H_j | O)} \tag{1.5} $$

Log-cotes et crédences pour encore faciliter les choses

La dernière étape va consister à travailler avec le logarithme des probabilités, qui permet de simplifier les calculs en remplaçant tous les produits par des sommes, et donne une échelle encore plus parlante. Si on considère le log en base 10, alors la log-cote de $H$ s'exprime ainsi :

$$logcote(H) = \log \frac{p(H)}{p(\neg H)} = \log p(H) - \log p(\neg H) \tag{1.6} $$

Une log-cote de 1 signifie que $H$ nous apparait 10 fois plus crédible que $\neg H$. Une log-cote de 2 signifie que $H$ est $10^2 = 100$ fois plus crédible, etc. À l'inverse une log-cote de $-1$ signifie que c'est $\neg H$ qui est 10 fois plus crédible que $H$.

On peut de même travailler avec les log-cotes relatives qui représentent directement à quel point $H_i$ est plus crédible que $H_j$ :

$$logcote(H_i, H_j) = \log \frac{p(H_i)}{p(H_j)} = \log p(H_i) - \log p(H_j) \tag{1.7}$$

Et on peut directement travailler avec le logarithme des probabilités non normalisées, qui sera donc défini à une constante additive près (plutôt qu'une normalisation multiplicative). Dans ce cas, on doit se focaliser sur des différences de log-probabilités non normalisées (et non plus des ratios) :

$$logcote(H_i, H_j) = \log \mathcal{P}(H_i) - \log \mathcal{P}(H_j) \tag{1.7}$$

Le Bayes-O-Matic, utilise beaucoup ces log-probabilités non normalisées et pour alléger la notation je les note $\mathcal{C}$ et les nomme crédences, car elles s'associent bien à la représentation interne qu'on peut se faire de nos croyances :

• elles sont logarithmiques, comme la plupart de nos perceptions
• elles sont peu interprétable seules, mais doivent être comparées les unes aux autres, de la même manière qu'on ne peut se détacher d'une croyance qu'en la remplaçant par une nouvelle croyance qui nous semble plus crédible

Avec ces nouvelles notations, le théorème de Bayes avec lequel on travaille va donc prendre une nouvelle forme :

$$\boxed{\forall i : \mathcal{C}(H_i | O) = \mathcal{C}(O | H_i) + \mathcal{C}(H_i)} \tag{1.8} \label{eq:bayes-c}$$

On peut difficilement faire plus simple, n'est-ce pas ?

Les réseaux bayésiens pour simplifier les expériences de pensée

Cependant la formule précédente cache encore beaucoup de complexité : le terme $\mathcal{C}(O | H_i)$ est en général loin d'être toujours évident à évaluer. Imaginez un cas réel : $H_1$ et $H_2$ sont respectivement la théorie de la gravitation de Newton et la théorie de l'univers géocentrique, et $O$ est l'ensemble des orbites observées des planètes dans le ciel. Comment évaluer $\mathcal{C}(O | H_1)$ et $\mathcal{C}(O|H_2)$ ? On ne sait même pas par où commencer.

Face à un problème aussi gros, la méthode la plus naturelle est de chercher à le découper en plusieurs sous-problèmes. Dans le cas des théories scientifiques, on peut chercher à faire des prédictions hiérarchiques : Si on suppose $H$, alors on peut avoir une prédiction intermédiaire $A$ et ses crédences $\mathcal{C}(A | H)$, et une autre prédiction $B$ avec $\mathcal{C}(B | H)$, et c'est en partant de $A$ et $B$ qu'on arrive enfin à prédire l'observation $O$ avec $\mathcal{C}(O | A, B)$.

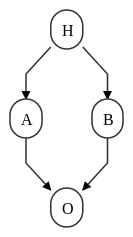
Représentation graphique des liens entre $H$, $A$, $B$ et $O$.

Concept général

Malheureusement, lorsqu'on commence à découper nos hypothèses en sous-hypothèses et prédictions ainsi, le théorème de Bayes ne va généralement pas garder sa forme gentille de \ref{eq:bayes-c}, et peut vite devenir difficile à calculer à la main. C'est à ce moment qu'entre en jeu un outil central : les réseaux bayésiens.

Un réseau bayésien est avant tout une représentation, un modèle. Il s'agit de représenter votre raisonnement sous la forme d'un graphe, comme sur l'image plus haut : avec des ronds et des flèches.

Chaque rond est ce qu'on appelle un nœud du graphe. Dans notre cas, il va s'agir d'une variable dont on peut chercher à déterminer la valeur. Par exemple, en reprenant le graphe plus haut :

• le nœud $H$ représente la ou les hypothèses initiales à comparer. Il peut prendre les valeurs $H_1$, $H_2$, $H_3$, … des différentes hypothèses incompatibles qu'on veut exprimer.
• le nœud $A$ peut être une prédiction intermédiaire, il pourrait par exemple s'agir d'une affirmation, qui pourrait alors avoir deux valeurs possibles : $Vrai$ ou $Faux$.
• le nœud $O$, l'observation, peut prendre une série de valeurs $O_1$, $O_2$, … représentant tous les résultats possibles qu'on imagine à l'expérience.

On va ensuite relier les nœuds ensemble par des flèches, que l'on nomme les arrêtes du graphe. Une flèche partant d'un nœud $X$ à un nœud $Y$ signifie que les valeurs crédibles de $Y$ dépendent de la valeur de $X$, et on dira alors que le nœud $X$ est un parent du nœud $Y$.

Attention, la présence d'une flèche signifie qu'il y a une relation logique entre les deux nœud, mais cela ne se traduit pas nécessairement par une relation causale au sens physique du terme.

Par exemple, on peut imaginer deux nœuds « Il a plu récemment » (Vrai/Faux) et « On voit des nuages dans le ciel » (Vrai/Faux). On peut tout à fait mettre une flèche du premier au second, en effet si on sait qu'il a plu récemment, on s'attent certainement à voir des nuages dans le ciel. Mais ce n'est pas pour autant que la pluie a causé les nuages, c'est en réalité le contraire.

Nous avons cependant une grosse contrainte dans la conception de notre graphe : il doit ne pas contenir de cycles. C'est à dire que si on se déplace de nœud en nœud en suivant les flèches, il ne doit jamais être possible de revenir à son point de départ.

Cette formulation en graphe correspond en réalité à une manière de factoriser une distribution de probabilité. En effet, si on a un graphe contenant $K$ nœuds $N^1, N^2, \dots, N^K$, notre connaissance globale de cet ensemble de nœuds doit être représenté par une distribution jointe $p(N^1, N^2, \dots, N^K)$. Mais une telle distribution est quelque chose d'énorme et complexe à manipuler. La représentation en réseau Bayésien revient à supposer une factorisation de cette distribution :

$$p(N^1, N^2, \dots, N^K) = \prod_i p(N^i | \pi_i) \tag{2.1}$$

Où $\pi_i$ représente l'ensemble des nœuds parents du nœud $N^i$. Par exemple, le graphe présenté comme exemple précédemment représente la factorisation suivante :

$$p(H, A, B, O) = p(H)p(A|H)p(B|H)p(O|A,B) \tag{2.2}$$

En procédant ainsi, on a donc séparé la grosse expérience de pensée initiale $p(O | H)$ en trois expériences de pensée plus petites : $p(A|H)$, $p(B|H)$ et $p(O|A, B)$. C'est là tout l'avantage qu'apporte la représentation en réseau bayésien : il devient possible de séparer un gros raisonnement en plusieurs étapes plus gérables.

Utilisation d'un réseau bayésien

Une fois qu'on a bien défini le graphe qui représente le mieux notre raisonnement, il faut alors effectivement faire les expériences de pensée associées à chaque nœud. Par exemple, pour le nœud $p(O | A, B)$, il nous faut fournir une probabilité pour chaque combinaison de valeurs possibles $p(O_i | A_j, B_k)$ du nœud et de ses parents.

Si un nœud a de nombreux parents, cela peut devenir un énorme travail, car le nombre de combinaisons de valeurs possibles devient énorme. On cherchera donc à privilégier des réseaux bayésiens où les nœuds on peu de parents, quitte à rajouter plus de nœuds pour séparer le modèle en plus de sous-modèles.

Une fois tout cela en place notre réseau bayésien est prêt à être utilisé, il n'y a plus qu'à observer la valeur de certains nœuds en faisant les expériences associées dans le monde réel, puis à appliquer le théorème de Bayes pour mettre à jour nos croyances sur les autres nœuds, que l'on ne peut pas observer directement.

Cette deuxième étape, l'application du théorème de Bayes, est dans le cas général un problème très complexe. Il s'agit même d'une question NP-difficile (on ne connait pas d'algorithme efficace la résolvant dans le cas général, et on ne sait même pas s'il en existe un). Cependant, il existe plusieurs algorithms qui peuvent en fournir des approximations correctes. L'un d'entre eux, qui est celui utilisé par le Bayes-O-Matic, est l'agorithme de propagation des convictions.

Cet algorithme calcule de manière approximée la distribution maginale à chaque nœud non observé. C'est à dire qu'il calcule pour chaque nœud $X$ la distribution $p(X | O^1, \dots, O^J)$, où $O^1, \dots, O^J$ représente l'ensemble des nœuds qui ont été observés.

Les limites de cet algorithmes sont surtout atteintes quand il y a des nœuds non-observés très corrélés entre eux, mais que l'état d'ensemble reste incertain. Par exemple, si nos expériences de pensée devraient prédire qu'il est extrèment probable qu'exactement un nœud parmi $A$ et $B$ est vrai, mais que nos observations ne permettent pas de déterminer lequel. On peut toutefois s'attendre à ce que ce cas soit rarement observé en pratique pour notre usage : on cherche à concevoir nos expériences de sorte à connaitre au mieux la valeur de chaque nœud (et donc essayer de tester $A$ et $B$ séparément, par exemple.)

Par ailleurs, si le graphe que vous avez choisi ne contient pas de boucle même en ignorant le sens des flèches, alors l'approximation est en réalité un calcul exact, et vous pouvez accepter ses résultats en toute confiance.

Le Bayes-O-Matic : une application web pour faire vos propres réseaux bayésiens

L'application est accessible ici : Bayes-O-Matic si vous voulez manipuler l'app en suivant la suite de cette partie. Je vous propose de re-modéliser l'exemple qu'Hygiène Mentale avait choisi dans sa vidéo sur le bayésianisme.

Le jeu des dés

Supposez que j'ai avec moi un sac qui contient 5 dés : un à 4 face (et qui peut donc faire un nombre entre 1 et 4), un à 6 faces, un à 8 faces, un à 10 faces et un à 12 faces. Je prends au hasard un dé dans ce sac et je le lance plusieurs fois de suite en vous donnant les résultats obtenus, mais sans jamais vous montrer le dé. Vous pouvez utiliser la méthode bayésienne pour essayer de deviner quel est le dé que j'ai tiré du sac.

Commençons par modéliser cette expérience. Le nœud initial va représenter le dé que j'ai tiré. Je l'ajoute dans le Bayes-O-matic en cliquant sur « Ajouter un nœud », et j'y rentre le nom « Dé choisi ». Ce nœud pourra prendre les valeurs « D4 », « D6 », « D8 », « D10 » et « D12 ».

Le Bayes-O-Matic me demande ensuite de remplir les crédences $\mathcal{C}$ pour ce nœud. Comme tous les dés ont la même chance de sortir du sac, je peux laisser toutes les valeurs à 0 : l'application travaille en log-probabilités non-normalisées, donc seules les différences entre valeurs ont de l'importance. Si elles sont toutes à 0, cela veut donc bien dire que toutes les valeurs sont a priori equiprobables.

Je peux maintenant ajouter un nœud pour le résultat du premier lancer. Nommons le « Lancer 1 », il s'agira à terme d'un nœud que l'on pourra observer. Ce nouveau nœud peut donc prendre 12 valeurs différentes : les nombres de 1 à 12, et il aura pour parent le nœud « Dé choisi ». Le Bayes-O-Matic nous demande alors de remplir un grand tableau de 5x12 entrées pour définir les crédences de l'expérience de pensée de ce lancer de dé.

Ce tableau se remplit ligne par ligne, et les crédences ne se comparent qu'au sein d'une même ligne, qui représente une valeur possible du nœud parent. Prenons la première ligne, « Dé choisi = D4 ». Si on a choisi un dé à 4 faces, alors les nombres de 1 à 4 ont la même chance de sortir, mais les autres nombres ne peuvent pas sortir. Pour refléter ça on peut comme précédemment laisser les cases des 4 premières colonnes à 0, et mettre les autres à la valeur -inf, qui représente $- \infty$. il s'agit de l'équivalent logarithmique d'une probabilité à 0 : ce résultat est impossible.

On peut ensuite remplir la suite du tableau avec la même règle : -inf pour les résultats impossibles, et $0$ pour les autres.

Valeurs Parentes	C(1)	C(2)	C(3)	C(4)	C(5)	C(6)	C(7)	C(8)	C(9)	C(10)	C(11)	C(12)
Dé choisi = D4	0	0	0	0	-inf	-inf	-inf	-inf	-inf	-inf	-inf	-inf
Dé choisi = D6	0	0	0	0	0	0	-inf	-inf	-inf	-inf	-inf	-inf
Dé choisi = D8	0	0	0	0	0	0	0	0	-inf	-inf	-inf	-inf
Dé choisi = D10	0	0	0	0	0	0	0	0	0	0	-inf	-inf
Dé choisi = D12	0	0	0	0	0	0	0	0	0	0	0	0

Ne pas oublier ensuite de cliquer sur « Enregister les crédences » pour que l'application prenne ces modifications en compte.

Une fois ça en place, on peut déjà rentrer la première observation, mettons que le premier lancer à été un 7, que cela nous dit-il sur les probabilités de chaque dé choisi ? Pour ce faire, allons dans l'onglet « Fixer les observations » et mettons l'observation du nœud « Lancer 1 » à 7. Le nœud apparait maintenant en gras sur la représentation graphique à gauche, cela met en évidence que c'est un nœud qui a été observé.

Cliquons maintenant sur le bouton « Calculer les croyances ». Le Bayes-O-Matic par défaut nous affiche les log-cotes associées à chaque valeur possible du dé. Qui donc représente chacunes notre conviction que le dé choisi est celui-là plutôt qu'un autre. Le menu déroulant vous permet d'afficher plutôt les croyances $\mathcal{C}$ directement ou les probabilités, si vous préférez.

On note déjà que les log-cotes pour les dés à 4 et 6 faces sont à $-\infty$ : le réseau bayésien nous affiche une certitude absolue que le dé n'est pas à D4 ou un D6. C'est tout à fait attendu : il est impossible de faire 7 sur un de ces dés, ce n'est donc certainement pas celui que j'ai tiré du sac.

Si on regarde les autres valeurs, on note qu'elles sont encore assez proche de 0, mais la valeur est plus élevée pour le D8 que pour les D10 et D12. Comme le faisait déjà remarquer Hygiène mentale dans sa vidéo c'est également attendu : un D8 a plus de chances de faire 7 qu'un D10 ou un D12. Comme les résultats sont encore assez proches de 0 en terme de cote, cela peut être parlant d'afficher les probabilités correspondantes (3e choix du menu déroulant) : 41% pour le D8, 32% pour le D10 et 27% pour le D12. On est encore loin d'une certitude.

Mais on peut maintenant ajouter plus de lancer. Pour ne pas nous fatiguer à encore recopier le grand tableau, selectionnez le nœud « Lancer 1 » dans la liste, et appuyez sur « Dupliquer ». Cela va créer un nouveau nœud identique, que l'on pourra nommer « Lancer 2 ». Supposons que le 2e lancer a fait 4, rentrons cela dans les observations et recalculons les croyances.

Maintenant la log-cote associée au D8 a encore augmenté, alors que celle des D10 et D12 a diminué. Si on continue à ajouter de nouvelles observations (lancer 3, 4, 5) avec toujours un résultat entre 1 et 8, la log-cote que l'on associe au D8 va continuer à augmenter. Au bout de 3 lancers la log-cote du D8 devient positive, cela veut dire qu'on considère qu'il y a au moins 50% de chances que le dé soit un D8. Mais si on ajoute une unique observation plus grande que 8, l'hypothèse D8 s'effondre, et sa log-cote tombe à $-\infty$.

Vous pouvez également ajouter un nœud de lancer suivant, mais ne pas lui mettre d'observation en laissant son selecteur sur la case vide dans l'onglet des observations. Alors dans ce cas le Bayes-O-Matic va également calculer des croyances pour la prédiction de ce que pourrait être le résultat de ce lancer de dé.

Autre examples et information mutuelles

L'application contient quelques autres exemples pré-définis (accessibles via le bouton « charger un exemple » en haut de la page). Chargeons l'exemple « morsure d'insecte » pour illustrer l'outil de l'information mutuelle.

Cet exemple très sommaire propose de manière un peu approximative de deviner quelle pourrait être la cause d'une piqûre d'insecte que l'on voit. Les crédences rentrées dedans sont sorties au doigt mouillé, pour illustrer. Allez à l'onglet des observations et retirez-les toutes, comme si rien n'avait encore été observé.

Allez maintenant à l'onglet « Information mutuelle » et selectionnez le nœud « Mordu par » comme base s'il ne l'est pas déjà. Vous voyez l'application afficher des scores pour les autres nœuds. Ces scores représentent la quantité d'information que vous gagneriez sur le nœud cible (« Mordu par ») si vous observiez la valeur du nœud associé à ce score. L'information est ici mesurée en bits. De manière générale, gagner un bit d'information permet approximativement de diviser par deux le nombre de choix possibles. Pour départager les 4 insectes candidats avec une certitude absolue, il nous faudrait donc 2 bits d'information. Mais on ne pourra jamais les obtenir, car la certitude absolue est quelques chose de très rare sur les terres bayésiennes.

On voit toutefois que les nœuds « Douleur » et « Démangeaisons » ont un bon potentiel de gain d'information, alors que le nœud « Gonflement » beaucoup moins. Il a l'air donc plus intéressant de remplir ces nœuds en priorité.

C'est là ce qu'apporte le calcul d'information mutuelle : si on a plusieurs expériences envisageables, ce score nous permet de faire en priorité celles qui vont probablement apporter beaucoup d'information. Autant dans cet exemple simple on peut facilement remplir tous les nœuds, autant dans des cas plus gros et complexes, il n'est peut être pas envisageable de faire toutes les expériences. Dans ce cas, on peut faire en priorité les expériences qui apportent le plus d'information pour un moindre coût.

Notez qu'une fois des observations ajoutées, il faut recalculer les informations mutuelles ! Le gain potentiel d'information dépend de ce que l'on sait déjà, et en général observer un nœud va réduire le gain d'information potentiel de tous les autres, et en particulier pour ceux qui correspondent à des expériences similaires à celle que l'on vient de faire, car il y a peu de chances qu'elles apportent une observation très différente.

Le mot de la fin

Je laisse ce Bayes-O-Matic à disposition de tous, en espérant qu'il puisse être utile. Vous pouvez également, à chaque nœud et à chaque ligne de vos tableaux de crédences écrire des commentaires pour justifier vos choix de valeurs. Et les boutons « Exporter en JSON » et « Charger depuis du JSON » vous permettent de sauvegarder, charger, et partager vos réseaux bayésiens.

Il n'est pas fini, je vais continuer à l'améliorer (à commencer par son style graphique, qui est encore très... simple). Si vous voulez me proposer des suggestions, voire participer au développement, l'application contient un lien vers Github, où elle est hébergée.

Bonne fin d'été à vous !